Каталог статей

Однако из-за слабой информационной связи между радиолюбителями - конструкторами в литературе появляется информация настоятельно рекомендующая устаревшую методику [1], например в [ 3]. Поэтому постараюсь по-возможности кратко изложить основы методики [2].

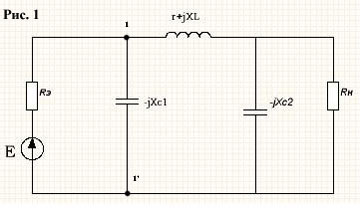
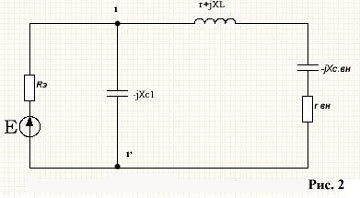
Принципиальная схема П-к на рис.1 может быть упрощена заменой параллельного соединения конденсатора C2 и резистора Rн на эквивалентное последовательное соединение зависимых от частоты внесенных сопротивлений r_вн и x_с.вн:

 Rн × XC22
 rвн = ----------- ; (1)
 Rн2 + XC22 


 Rн2 × XC2
 Xc.вн = ----------- ; (2)
 Rн2 + XC22 
 

Согласно рис.2 положим, что эквивалентное индуктивное сопротивление второй ветви (рис.2) X_LЭ = X_L - x_c.вн; r = r_L + r_вн. Тогда комплексная входная проводимость в точках 1 и 1':

 1 1 1 1 r - jXLЭ 
 ---- = ----- + --------- = j ----- + ---------- . 
 Zвх -jXC2 r + jXLЭ XC2 r2 + XLЭ2 

В последнем выражении мы избавились от мнимости в знаменателе. Запишем его в виде:

 1 r 1 XLЭ 
 ---- = --------- + j (---- - ---------) . (3)
 Zвх r2 + XLЭ2 XC2 r2 + XLЭ2 

На резонансной частоте (ω = ω_р) входная проводимость чисто активна и равна проводимости источника 1 ⁄ R_э, а мнимая часть = 0:

 1 r 
 --- = ----------- (4)
 Rэ r2 + XLЭ.р2 

 r2 + XLЭ.р2 = XLЭ.р × XC1.р . (5)

Следовательно,

 1 r 1 
 ---- = ------------ = ----------, 
 Rэ XLЭ.р × XC1.р Qн × XC1.р

 
 XLЭ.р 
 Qн = ----- 
 r

Тогда,

 RЭ
 XC1.р = ----- . (6)
 Q н

Так как

 1 Q н
 ----- = ωрС1 = ----,
 XC1.р RЭ

Значение X_LЭ.р = r Q _н подставим в (4) и находим:

 RЭ
 r = ---------. (7)
 QH2 + 1

Заметим, что КПД П-к η = r_вн ⁄ r , а из (1):

 Rн XC22
rвн = ηr = ----------.
 Rн2 + XC22

Следовательно,

 Rн
XC2p = ------------------ (8)
 Rн 
 √(----- - 1)
 (ηr)

На основании вышеизложенного: X_L = X_LЭ + X_с.вн; X_LЭ = r Q_H;

 Rн
Xс.вн = rвн ---- см. уравнения (1) и (2). 
 XC2

Поэтому,

 Rн
XL = rQH + rвн ----.
 XC2

Так как r_вн = η r, то

 Rн
XLp = r(QH + η -----). (9)
 XC2p

Формулы (6), (7), (8), (9) позволяют найти значения величин элементов П-к с потерями для данной резонансной частоты. Полоса пропускания такого несимметричного по нагрузке фильтра увеличивается с уменьшением Q_H. Для симметричных фильтров, без учёта потерь, минимум коэффициента передачи напряжения в области пропускания находится на относительной частоте Y_min = 1 ÷ √ 3. Формулы данной методики точны и много проще формул по методике [1].

Продолжим обсуждение вопроса. При симметричной нагрузке (R_Э = R_н) в режиме согласования П-к должен быть симметричным, что следует из (6) и (8). При отсутствии потерь в П-к выходные напряжения в начале АЧХ и на частоте резонанса, естественно, совпадают, а в полосе пропускания появляется некоторый «завал» в виде седловины, увеличивающийся с увеличением Q_н. Можно показать, что независимо от Q_н, минимум седловины находится на относительной частоте ω_min ⁄ ω_P = Y_min. В таблице показана зависимость нормированного коэффициента передачи напряжения K_min(Ymin), как функции Q_H (вторая строка таблицы).

При выборе промежуточных точек достаточна линейная интерполяция. Как показано в (2), минимум седловины не зависит от R. Из таблицы видно,что фильтр нижних частот с приемлемой равномерностью имеет низкую добротность нагруженного контура и, только в этом случае, может применяться в широкополосных фильтрах.

Строго говоря, расчёт таблицы проведен для η = 1. Из (6), (7), и (8) следует, что Х_C1 не равняется X_C2, и максимум неравенства увеличивается с уменьшением Q_H. Расчёт для η = 0.95 и Q_H = 1 (меньшее значение применять не следует) - погрешность не превышает 5 %, что вполне допустимо при радиотехнических расчётах.

Если Q_H > 5, то фильтр образует узкополосную систему с глубоким провалом седловины, с лучшей фильтрацией высших гармоник и ухудшенной фильтрацией низких частот вне рабочего диапазона и субгармоник. Следует заметить, что методика расчёта [1], в отличие от предлагаемой, не работает при симметричной нагрузке. Проверка для Q_H = 2, R=50 Ом, η = 0.95 по методике [1] показывает, что:

 50 - 0,95 × 50 
XC2 = -------------------------------- = 4,378997 Ом;
 1
 √----- × (5 - 0,952) - 2 - 0,95 
 0,95

 50 
XC1 = ---------------------- = - 5,651148 Ом.
 (2 × XC2 - 0,95 × 50) 

По методике [2], X_C1 = 50 ÷ 2 = 25 Ом. Правильные методики не могут дать разных результатов. Но методика [2] обоснована в настоящем материале, в то время, как автор [1] в своей работе указывал на приближённость его метода расчёта, основанного на предположении, что КПД П-к

 QH 
 η = 1 - -----, 
 QXX 

При симметричной нагрузке R_н = R_э фильтр в виде П-к не симметричен (X_c1 ≠ X_c2):

 RЭ2 RН2 = RЭ2 
 Xc1p2 = ----, Xc2p2 = ---------- ,
 QН2 QН2 1
 ---- + ---
 η η 

Для широкополосных ФНЧ погрешность вполне допустима при радиотехнических расчётах, используя таблицу. При симметричном П-к (X_c1р = X_c2р) нагрузка, как мы видели, будет симметричной только в случае η = 1.

В общем случае из равенства X_c1p² = X_c2p² находим (применим (6), (7), (8)):

 RH RH 1 RH 
 QH2 × ---- ( ---- - --- ) = ------ - 1.
 RЭ RЭ η η × RЭ

При η = 1:

 QH2 × RH RH 
 (--------- - 1) × (--- - 1) = 0
 RЭ RЭ

В последнем случае симметричный П-к может работать на согласованную нагрузку не только при R_н = R_э, но и при R_э ÷ R_н = Q_н²; тогда X_c1р = X_c2р = X_Lр. Такой П-к обычно называют антиметричным. В общем случае (η ≠ 1) коэффициент трансформации R_н ÷ R_э находится из предыдущего равенства.

Таким образом, симметричные фильтрующие системы с П-к, строго говоря, не существуют. Однако применение расчётных формул в предположении η = 1 с приемлемой для практики точностью более удобны. Кроме тех случаев, когда требуется определить потери в самом П-к, которые при малых добротностях достаточно малы.

Важный вопрос, когда можно пренебречь величиной

 rвн 
 η = --------- ? 
 rL + rвн

Расчёт показал, что для η ≥ 0.95, необходимо иметь r_вн ≥ 20 r_L. Определение величины r_L теоретическим расчётом сложно, и для каждого диапазона находится из опыта и литературных рекомендаций.

Следует заметить, что в учебнике для ВУЗов (Радиопередающие устройства. Под ред. М.В. Благовещенского и Г.М. Уткина, М.: Радио и связь, 1982) добротностью нагруженного контура названа добротность катушки индуктивности П-к на резонансной частоте: ω_рL ÷ r_L = Q. При этом влияние X_с.вн в ветви с катушкой индуктивности фактически отбрасывалось. Конечно, автор имеет право дать название исследуемому им явлению. Но утверждать при этом, что КПД П-к

 Qн 
 η = 1 - -----, 
 QXX

 ωp L ωp L 
 Qн = --------, QXX = ----- 
 rL + rвн rL

Пример расчёта широкополосного фильтра

Дано: верхняя частота полосы пропускания f_в = 7.2 МГц; К_{н(Υmin )} ≥ 0.9; R_э = R_н = 50 Ом; η ≈ 1.

Находим Q_н, которая в таблице согласно заданной неравномерности в полосе пропускания находится в пределах 1.6<Q_н<1.8. Применив линейную интерполяцию, находим требуемую Q_н = 1.6939.

А можно просто построить по таблице кривую зависимости К_{н(Υmin )} от Q_н и работать с ней. Тем более, что эта зависимость линейна в диапазоне 1.1<Q_н<3, и расчёт можно выполнить по формуле

 a - Кн(Υmin )
 Qн = -------------- ,
 b

Последнее выражение получено из (11) и (8). Далее требуется найти ω_p = 2πf. Можно показать, что для симметричного П-к Υв = ω_в÷ω_p = 2Υmin. Следовательно,

 ωв 2π×7,2×106
 ωp = ------ = ---------- = 39,17806×106 
 2Υmin 1
 2×-----
 √3

Пример расчёта узкополосного фильтра

Для узкополосного фильтра главное – это фильтрация высокочастотных гармоник. А для сравнительно узкополосных любительских диапазонов ширина полосы пропускания не имеет решающего значения. Могу показать, что коэффициенты передачи напряжения (АЧХ) в согласованном режиме при прямом и обратном включении отличаются лишь постоянным множителем:

 R1
 KUобр. = KUпр. ---. 
 R2

Чем больше величина Q_Н, тем больше провал в седловине и лучше фильтрация высших гармоник, которая, как показано в [4], улучшается также с увеличением отношения R_Н ⁄ R_э.

При увеличенных Q_Н радиолюбители часто отмечают снижение выходной мощности усилителя в высокочастотной области КВ диапазона, особенно в усилителях на лампах с высоким R_э. Возможно потому, что минимальная входная ёмкость С1 примерно 50 пф. На резонансной частоте

 1 RЭ
 ХС1р = ----- = ----. 
 ωp С1 QН

Поэтому при больших значениях R_Э требуется увеличение Q_Н, что может привести к падению КПД П-к и, соответственно, усилителя. В случае применения усилителя на мощных транзисторах его выходное сопротивление достаточно мало, что и снимает эту проблему.

Пример:

 rL
η = 1 - --------- , 
 rL + rВН

 1 
т.е. ----------- = 0.05 или rL < rВН/19.
 1 + rВН/rL

 RH X2C2P
rВН = ----------- . 
 R2H + X2C2P 

Далее из (9) и (10) находим:

 75
XC2P = --------------- = 18.2467 Ом. 
 75
 √-----------(132+1)-1 
 0.95 * 750

Следовательно, необходимо иметь r_L < 0.220588 Ом.

Если катушка индуктивности рассчитана и изготовлена, её добротность Q_L (это не Q_Н) можно измерить, например, методом последовательного резонанса с учётом того, что добротность конденсатора практически всегда более чем на порядок (10 раз) выше добротности катушки индуктивности. Зная Q_L, можно вычислить r_L = X_Lр / Q_L. Измерения надо проводить в реальных условиях работы, с учётом, например, влияния короткозамкнутых катушек соседних диапазонов. Особое внимание при настройке обратить на возможное влияние анодного дросселя на резонансную систему [5].

Далее находим: Х_С1р = 750 / 13 = 57.6923 Ом, Х_С2р = 18.2467 Ом,

 750 0.95 * 75
ХLр = -------- (13 + ----------) = 74.5800 Ом. 
 132 + 1 18.2467

 1 1 
С1 = ------- = ----------------------------------- = 129.973 пф
 ωp ХС1р 2π*0.5 (21*106+21.450*106)*57.6923 

 1
С2 = ------- = 410.949 пф
 ωp ХС2р

 ХLр
L = ----- = 0.559235 мкГн
 ωp

Если Вы устали от формул ниже по ссылке более простой способ решить эту проблемку

Расчет П-контура

Приведенный калькулятор избавит вас от расчетов вручную. В нем принято, что холостая добротность C1 и С2 намного выше, чем у L. Для большинства конденсаторов это справедливо.

Увеличение нагруженной добротности П-контура Qн увеличивает подавление гармоник и ёмкости конденсаторов (важно при лампе с большой ёмкостью), но снижает КПД.

Для выходного П-контура усилителя R1 ≈ Ea/2,1•Iа (Ea – постоянное напряжение, Iа - постоянный ток анода), или R1 ≈ (0,9Ea)²/2P (P – выходная мощность). Для входного П-контура РА с общей сеткой R2 ≈ 1/S (S – крутизна лампы).

Подставьте свои значения R1, R2, F,  Qн  (для ламп  10...20,  транзисторов 2...10), Qхх катушки,  мощности источника сигнала.      Рабочая частота F  MHz Холостая добротность катушки Qхх Нагруженная добротность П-контура; Qн Мощность передатчика Р    Ватт L µГн   Ток в L А   Источник           R1 Ом              Нагрузка        R2 Ом Рвых Вт   КПД %   C1 пФ           C2 пФ Реактивная мощность в С1 ВАр    В С2   реактивная мощность, ВАр

Для оценки конструктивных требований к деталям П-контура выдается ток в катушке (исходя из него надо выбирать провод) и реактивная мощность (она измеряется в ВАр - Вольт-Ампер-реактивных) в обоих конденсаторах. Для конденсаторов, за исключением вакуумных и воздушных, справедливо правило: если в паспорте конденсатора не указана реактивная мощность, то такой конденсатор не предназначен для работы в мощных ВЧ-контурах  и скорее всего сгорит при попытке его использования (впрочем, слюдяные КСО  и без обозначения выдерживают пару-тройку сотен реактивных ватт и подойдут для относительно маломощных контуров). 

 Для работы калькулятора у вас в браузере должна быть включена JAVA. Как и все программы на JAVA данный калькулятор может свободно копироваться и дорабатываться, при соблюдении единственного условия - явной ссылки на эту страницу.

Калькулятор снабжен подсказками и развитыми сообщениями о возможных ошибках, поэтому разобраться с ним трудностей не представляет – просто подставьте исходные данные. Разделитель в цифрах – точка, запятую в цифрах программа воспринимает как букву, поэтому не понимает что делать с такой цифрой. Калькулятор работает по формулам, приведенным UA3DA в [1].

Хотел бы отметить, что популярная в  методика расчета П-контура по среднегеометрическому сопротивлению  (она, например, описана в статье UA9ACZ "О помехах телевидению" и используется в большом числе программ, в том числе до 30.09.2007 она применялась в калькуляторе этой странице) дает не очень точные результаты в смысле согласования. На это обратил  моё внимание  человек с ником Игорь 2 с форума, за что я ему признателен.

Дополнение от 12.09.2009: В соответствии с рекомендациями UA3SDE (спасибо, Сергей!)  калькулятор подправлен, и теперь работает в любом направлении трансформации сопротивлений (при R1 > R2, R1 < R2 и R1 = R2). Исключение составляет лишь одна точка (в ней формулы UA3DA дают неопределенность), в которой R1/R2 в точности равно КПД.  Но это случай, скорее умозрительный (повышать сопротивление на несколько % П-контуром практически ни к чему). Кроме того,  если Вы в эту неопределенность умудритесь попасть, то она полностью исчезает (т.е. формулы и калькулятор продолжают давать корректные результаты) при изменении любого из параметров R1, R2, Qн и Qхх на очень малую (вроде 0,1%) величину.
 

   Меня спрашивали, почему убран, имевшийся ранее, расчет подавления второй гармоники? Дело в том, что полный расчет по АЧХ слишком ресурсоемок для Java Script. А простейшая формула (которая ранее использовалась в калькуляторе), что подавление второй гармоники в разах составляет 6Qн является весьма приближенной. И часто понимается и применяется неправильно.

1. На самом деле подавление зависит еще и от Qхх и от величин R1 и R2. Погрешность упомянутой формулы в диапазоне добротностей Qн = 6 ... 30 и R1 = 200 .... 5000 Ом составляет  + 1..1,5 дБ  (что явно не тянет на прецизионные расчеты с выводом знаков после запятой) и быстро нарастает  до нескольких дБ с уменьшением Qн. Причем нарастает в плохую сторону, формула обещает лучшее подавление, чем получается на самом деле.

2.   Мало кто знает, но формула 6Qн относится не к одному П-контуру. Она применима лишь к системе: лампа, работающая в режиме В (т.е. с углом отсечки 90⁰)  + стоящий следом за ней П-контур. Т.е. в ней учтено, что вторая гармоника на входе уже сама по себе (из-за свойств режима В) примерно на 7,5 дБ меньше первой. 

Так, что если Вы считает обычный ламповый РА (отсечка 90⁰), то того, чтобы на выходе уровень второй гармоники был ниже первой на 40 дБ (т.е.  в 100 раз) потребуется Qн ≈ 16  (тут получается 100 ≈ 6 •16).  

Литература

1.  К. Шульгин, UA3DA. Методика расчета П-контура передатчика. Радио 1985, N5, стр. 15 - 17.